Как-то раз, беседуя с сотрудником на работе, разговор зашел за динамические головки с обратной связью. До того момента я даже не слышал об этом, но данная тема меня сильно заинтересовала сразу же. Общепринятое название этому ЭМОС: электро-механическая обратная связь. Суть в следующем: на НЧ динамическую головку устанавливается датчик, по показанием которого адаптивная система выполняет расчет необходимой формы и амплитуды управляющего сигнала, который подается на катушку динамика. Все это сделано для того, чтобы улучшить звучание акустической системы, особенно на низких частотах.
Далее по тексту будет идти теоретическое описание системы ЭМОС, причем сухим научным языком, так что извиняйте :))) Добавлю лишь небольшой спойлер: в железе это уже собрано в виде первого макета и кое-какие результаты получены. Практическая часть будет описана немного позже, когда будут получены достоверные измерения акустики и сделаны доработки аппаратной части.
P.S. импорт документа с формулами из Word в WordPress — это боль))
Версия статьи в формате .PDF: ЭМОС Часть 1. Введение
Введение
ЭМОС (электромеханическая обратная связь) – один из технических приемов улучшить характеристики акустической системы, основанный на введении обратной связи по одному из физических параметров подвижной системы динамической головки. По факту, данный прием является внедрением ПИД-регулятора в акустическую систему.
Обратная связь может быть реализована по перемещению, скорости, либо ускорению диффузора динамика. В данной статье основное внимание будет уделено обратной связи по ускорению. Для введения такой обратной связи динамическая головка должна быть подвергнута модернизации, а именно установки датчика ускорения на звуковую катушку, подобно тому, как это описано в [1-3]. Такое расположение датчика связно с тем, что точку изменения ускорения необходимо разместить как можно ближе к моторной части динамической головки для уменьшения влияния запаздывания распространения сигнала по материалу диффузора и уменьшению сдвига фазы между ускорением звуковой катушки и измеренным сигналом ускорения a(t).
Уравнение движения диффузора
В первом приближении представим динамическую головку как пружинный маятник, уравнение движения которого имеет следующий вид:
(1)
Зная, что первая производная координаты по времени есть скорость, а вторая – ускорение, перепишем данное уравнение в таком виде:
(2)
где: m – масса подвижной системы динамика
– коэффициент затухания собственных колебаний диффузора k – жесткость подвеса диффузора
– сила, которую прикладывает звуковая катушка к диффузору, при протекании через нее электрического тока
Выражение (2) не учитывает такие параметры системы, как акустическое оформление, паразитные резонансы, зависимости 
, k от величины отклонения 
, электрическое демпфирование звукового усилителя, и т. д., однако, для начальных этапов исследования ЭМОС этого достаточно.
Обратная связь
Звуковое давление (SPL) создает ускоренное движение диффузора динамика, поэтому, логично выбрать обратную связь именно по ускорению, как это и сделано в [1-3], однако, это совсем не обязательно, так как перемещение, скорость и ускорение являются зависимыми величинами, и обратную связь можно реализовать по любой из перечисленных величин.
Дальнейшие математические выкладки будут повторять работу [6], с тем отличием, что в нашем случае обратная связь будет выполнена по ускорению, а не по скорости.
Ошибка регулирования будет описываться следующим выражением:
(3)
A(t) – заданный закон изменения ускорения (звуковой сигнал)
a(t) – фактический закон изменения ускорения (сигнал с датчика ускорения)
и ПИД-регулятор будет иметь следующий вид:
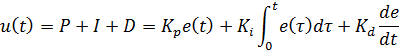(4)
Воспользовавшись выражением (2) и (4) «подключим» наш ПИД-регулятор к динамической головке таким образом:
и в результате:
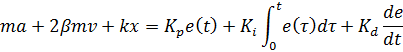(5)
В итоге мы получаем дифференциальное уравнение, которое описывает поведение динамической головки при использовании ЭМОС по ускорению. Дальнейшим этапом работы будет исследование системы (5) на предмет влияния каждой из компонент ПИД-регулятора на работу системы ЭМОС.
Пропорциональная компонента
Перепишем выражение (5), оставив в правой части только P-компоненту, и воспользуемся выражением (3):
Раскрыв скобки и приведя подобные получаем следующее:
(6)
Обратим внимание на 
. При отрицательной обратной связи по ускорению наличие пропорциональной компоненты увеличивает эффективную массу подвижной части динамической головки, что влечет за собой уменьшение резонансной частоты динамика. В принципе, подобный эффект можно как-то использовать при конструировании акустики, но в нашем случае это не несет никакого полезного эффекта.
Дифференциальная компонента
Проделаем все вышеописанные операции для дифференциальной компоненты ПИД-регулятора:
(7)
В данном случае в ходе дифференцирования ускорения по времени мы получаем такую интересную вещь, как функцию рывка [7]. Лично я не могу дать физическое обоснование данной функции, в первой итерации изучения системы ЭМОС я опущу дифференциальную компоненту без какого-либо обоснования.
Интегральная компонента
По аналогии рассмотрим интегральную компоненту ПИД-регулятора:
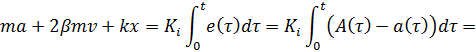
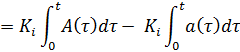(8)
С интегралами будет посложнее. Для начала рассмотрим первый интеграл отдельно: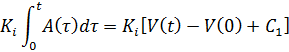
— в нашем случае это сигнал с выхода звуковой карты, который описывает форму изменения ускорения диффузора динамика. При операции интегрирования мы получаем функцию изменения скорости. В результате этого мы получаем две константы: первая это константа интегрирования 
, а другая это значение скорости в начальный момент времени 
. С этими константами мы разберемся позже.
Аналогичным способом высчитываем второй интеграл:
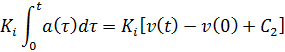
Подставляем полученные значения в уравнение (8):
(9)
Раскрываем скобки и приводим подобные:
(10)
Давайте разберемся, что мы получили в итоге. Коэффициент 
дает добавку к 
, что по факту является увеличением коэффициента затухания собственных колебаний подвижной системы динамика. Следовательно, наличие интегральной составляющей увеличивает коэффициент демпфирования динамической головки. Для того, чтобы двигаться дальше, давайте разберемся с
, 
и 
— значение заданного закона изменения скорости (интеграл от звукового сигнала) в начальный момент времени, – скорость диффузора в начальный момент времени. Интегратор, который лежит в основе интегральной части ПИД-регулятора, имеет свойство «запоминать» всю свою предысторию (так как у нас диапазон интегрирования от 0 до t). Нам это не нужно, так как эти значения будут создавать постоянную составляющую на звуковой катушке динамика. Поэтому, в аппаратной реализации нам надо будет принять меры, которые будут нейтрализовать накопление постоянной составляющей в интеграторе. Таким образов, в выражении (10) мы можем 
, 
и приравнять к нулю. В результате получаем выражение для ЭМОС с интегральным звеном в окончательном виде:
(11)
Давайте рассмотрим, как будет вести себя И-регулятор в случае, если диффузор точно повторяет заданный звуковой сигнал:
В этом случае сигнал ошибки (3) будет обращаться в ноль (
), и выражение (8) будет иметь вид:
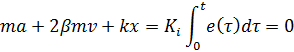
Таким образом, судя по нулевому значению в правой части выражения и отсутствии какой-либо добавки к коэффициенту затухания 
, приходим к выводу, что если закон изменения ускорения диффузора точно повторяет звуковой сигнал, то И-регулятор не будет оказывать какого-либо влияния на звуковую катушку динамика.
Выводы
В результате вышестоящих умозаключений приходим к выводу, что в системе ЭМОС с обратной связью по ускорению оптимальным решением будет применение интегральной компоненты ПИД-регулятора, так как наличие этой компоненты увеличивает коэффициент затухания собственных колебаний подвижной системы динамика, тем самым уменьшает величину паразитных резонансов акустической системы в целом. Причем величина демпфирования динамика является динамической по величине, и чем больше мгновенное значение невязки (3), тем выше значение коэффициента демпфирования.
Вывод о необходимости применения интегратора полностью совпадает с мнением автора цикла статей про ЭМОС [1-3], причем один и тот же результат получен разными методами анализа системы ЭМОС.
Обратная связь по координате
В [8, 9] представлен пример НЧ колонки с положительной обратной связью по давлению внутри закрытого ящика. Как показано в [9], при данной обратной связи эффективная жесткость подвеса динамической головки уменьшается. Давайте попробуем построить математическую модель данной системы управления, выполним ее анализ, и сверим полученный результат с поведением системы, представленным в [8, 9].
В первом приближении примем давление внутри закрытого ящика как линейную функцию перемещения диффузора динамика. Это будет справедливо с достаточной точностью для низкочастотного диапазона звуковых колебаний. В этом случае ошибка регулирования будет иметь следующий вид:
(12)
где:
— звуковой сигнал
— перемещение диффузора динамика
По аналогии с выражением (5), запишем уравнение движения диффузора динамической головки с положительной обратной связью, описанной формулой (12):
Раскроем скобки и приведем подобные:
(13)
В результате, согласно (13) получаем, что наличие подобной обратной связи приводит к уменьшению эффективного коэффициента жесткости подвеса подвижной системы динамика, что и было продемонстрировано в материале [9]. Этот результат является косвенным доказательством правильности подхода к описанию поведения системы ЭМОС и верным выводам, полученным в конце данной статьи. Однако, для продолжения исследований в данном направлении требуется аппаратная реализация описанной системы ЭМОС и последующее ее изучение.
Литература
- ЭМОС: коротко обо всем [Электронный ресурс] // Мухамедзянов Н. (aka Nota Bene). [2012] URL: http://reanimator-h.narod.ru/faq_emos.htm
- Вниз по лестнице, ведущей вверх… или ЭМОС в низкочастотном звене АС. [Электронный ресурс] // Мухамедзянов Н. (aka Nota Bene). URL: http://reanimator-h.narod.ru/emos.html
- ЭМОС в сабвуфере — generation next [Электронный ресурс] // Мухамедзянов Н. (aka Nota Bene). [2009-2010] URL: http://reanimator-h.narod.ru/emos_gn.htm
- ПИД-регулятор [Электронный ресурс] // Википедия. URL: https://ru.wikipedia.org/wiki/%D0%9F%D0%98%D0%94-%D1%80%D0%B5%D0%B3%D1%83%D0%BB%D1%8F%D1%82%D0%BE%D1%80
- Оптимизация электронной схемы модулятора Мессбауэровского спектрометра // Петин Г. П.
- Новая система допплеровской модуляции мёссбауэровского спектрометра [Выпускная квалификационная работа] // Сивоконь Д. Н. [2017] URL: https://dimoon.ru/wp-content/uploads/2021/08/diplom_final.pdf
- Рывок (кинематика) [Электронный ресурс] // Википедия. URL: https://ru.wikipedia.org/wiki/%D0%A0%D1%8B%D0%B2%D0%BE%D0%BA_(%D0%BA%D0%B8%D0%BD%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)
- Feedbass! (microphone in loudspeaker) [Электронный ресурс] // DeepSOIC (Victor Titov) [2018] URL: https://hackaday.io/project/68980-feedbass-microphone-in-loudspeaker
- Как настраивать ЭМОС типа feedbass [Видеоролик] // DeepSOIC (Victor Titov) [2018] URL: https://youtu.be/bgoJ-FIFCl4